(Michael Chinen)

The choice of a window in a discrete Fourier transform (DFT) is an art due to tradeoffs that it implies. When the time domain signal with a single frequency (e.g. a sine-tone) is transformed into the frequency domain, it creates a lot of other ‘phantom’ frequencies called sidelobes. The no-window choice of the rectangular window has a -13 dB sidelobe whenever the frequencies of the signal are not perfectly divisible by the window length (but when they are there are no sidelobes). In practice, for audio processing, I see Hann and Hamming windows being used. The Hamming window is my personal favorite due to a very high sidelobe rejection of over -40 dB, and has a raised edge, which destroys less information. Also Richard Hamming is cool (cf. see: Bell labs – Shannon’s manager and the famous asker of the ‘Hamming Question’) .

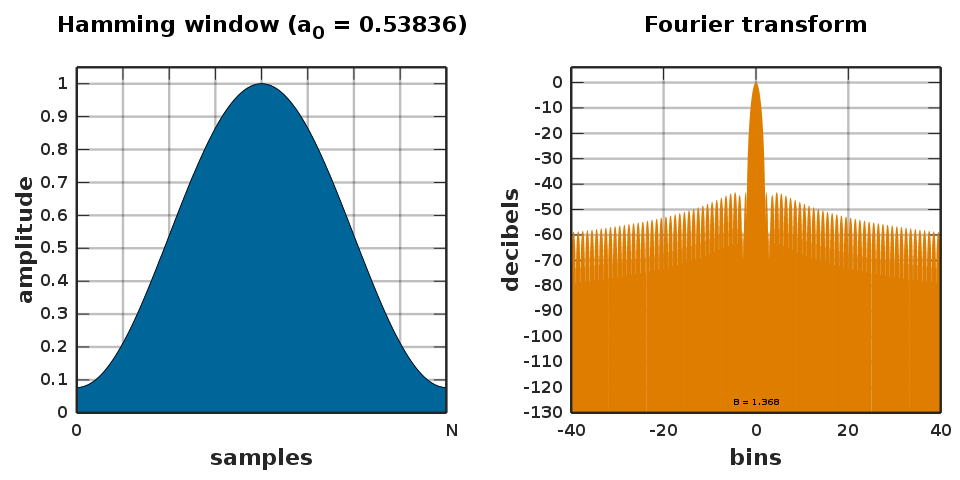
When I think about windows I usually think about the Fourier transform of these windows. But they don’t tell the full story. Phase, as usual, complicates everything. Notice how the sidelobes are themselves periodic. Without even analyzing anything, this implies there is some complex rotation going on, and the DFT is just ‘sampling’ this rotation at regular intervals. This is why you can use a rectangular window on a signal with a certain frequency and get no windowing artifacts or sidelobes – in this case the sampling/aliasing of the window happens to fall exactly where the complex values are the same. So as you move away from the exactly-aligned frequency to other frequency, the sidelobes ‘pop’ into existence.

Generally, DSP practitioners just pick one window for an application and stick to it. In theory, we could use an adaptive window to reduce sidelobe confusion, but it is not simple. Using an convolution directly on the waveform in ML processing is effectively assuming a fixed window, (and often comes with windowed preprocessing) as in TasNet or wav2vec. Something about this feels like a Bayesian problem since the choice of window provides different uncertainties conditional on the application and properties of the signal. It’s fun to think about how an adaptive window might work. Adaptive filters are fairly common, of course (and virtually all ML-processing is adaptive), but somehow the first thing that touches the signal – the window – is more difficult to touch. Perhaps this has to do the the relative stability that a fixed window brings. But if you look at picking the window for each frame to reduce the uncertainty. The ‘easy’ way out, is to use a very high sampling rate and/or Mel spectrogram, which smoothes out the sidelobes considerably for the high frequencies. Anyway this is a brainstorm, and something to look at further in the future.

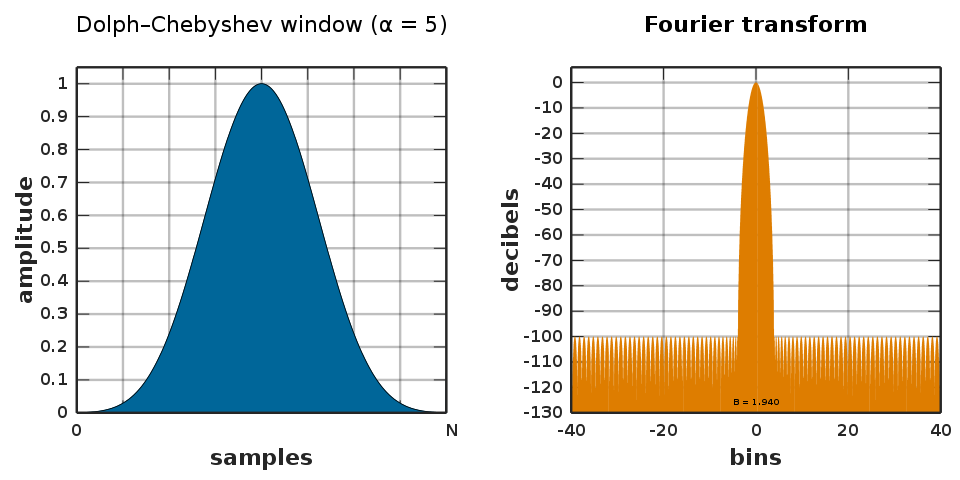
The other thing I want to dig further into is the complex phasor for these windows. In other words, how the real and imaginary values evolve with respect to frequency for the window. My guess is that it looks a lot more steady than the sidelobes in the typical magnitude frequency domain that we commonly look at, especially if we looked at the Dolph-Chebyschev window which is designed to have flat sidelobes. This is not a big leap in perspective, and probably something people have looked at, but I don’t recall it being discussed in my signal processing education. I’d like a 3blue1brown-style animation of this.

‘Uncertainty’ as a word is very useful in talking about probability theory to the general public. Because we associate fear and doubt and other emotions with uncertainty in the casual usage, the word immediately gets across the point that at least some of the variance is due to the observer’s mental state, which translates well to the concept of prior information. But how much of the uncertainty in a random variable or parameter is due to uncertainty, and how much is actually in the process.

Edwin Thompson Jaynes’ chapter 16 of Probability Theory: The Logic of Science (16.7 What is real, the probability or the phenomenon?) is very explicit in saying that believing randomness exists in the real world is a mind projection fallacy. The projection is that because we things appear uncertain to us, we believe the generating process itself is random, rather than appreciating our lack of information as the source of the uncertainty. We had a discussion in our reading group about this – Jaynes being a physicist and all, it seems like a strong statement to make without qualifiers, since ‘true randomness’ might exist in quantum processes, like entanglement/wave functions, when an observer ‘samples the distribution’ by taking a measurement.

But if we take a step back, my reading group buddy mentioned that Jaynes’ field was closer to thermodynamics, not quantum mechanics. So maybe he was only considering particular ‘higher level’ aspects of the real world that have deterministic properties. But in many fields treating processes as stochastic is fairly common. Perhaps they don’t consider it as part of the real world or not, but usually humans don’t care about the territory as much as the map because the map is literally what we see. I suppose the problem with this approach is when we encounter Monty-Hall like paradoxes, which are surprisingly infrequent in the real world, probably because things are tangled up and correlated for the most part. Below are some examples from my world where the stochastic process is considered. I don’t find these problematic, but are kind of interesting to think about.

In discussions with machine learning/signal processing folk, sometimes I hear the distinction between stationary noise and signal, or between voiced and unvoiced speech as deterministic and stochastic, with attempts to model as such. My own group at Google even used such a strategy for speech synthesis. Here, ‘stochastic’ and ‘uncertain’ are interchangeable. If we knew the sound pressure levels of all points in the past millisecond within the 21.4 cm (343 m/s speed of sound divided by 16 kHz sample rate), we would be able to predict the next sample at the center of the sphere with higher accuracy, even if it was Gaussian noise. Jaynes believes this uncertainty can be reduced to zero with enough information. For this case, it’s much easier than quantum mechanics to see it as a deterministic process, since sound is mostly just pressure waves moving linearly through space.

Another connection from my perspective is the connection to process based ‘academic’ music, such as John Cage or Christian Wolff, and of course Iannis Xenakis, who explicitly references stochastic processes. Here, I think the term stochastic process tends to refer to explicit (as in Xenakis’ granular synthesis) or implicit (as in Cage’s sheet tossing in cartridge music or die rolling in other pieces). Die rolling music goes back at least as far as to Mozart’s Würfelspiel, but I think Mozart thought about it more as a parlor trick than an appreciation of randomness. The Cage vs Xenakis style can be considered from Jaynes’ pure determinism stance, and gets even crazier if you consider the folks that believe consciousness arises from quantum processes, since Cage/Wolfe often use the signalling/interaction between musicians to ‘generate entropy’.

I find that statisticians, or at least statistics literature tends to much more opinionated than other areas of STEM, like computer science and math to the point where it is quasi-religious, but I’m curious if insiders e.g. in pure math feel otherwise. Recent examples are Jaynes and Pearl, which make interesting arguments but survey histories with some preaching for at least a quarter of the text. It makes it interesting to read, but also difficult to know if I’ve processed it well. This book is full of great examples that I feel I will need to look at from other perspectives.

At the end of the day though, I’m uncertain (no pun intended) if the real world contains random processes, and how these might bubble up to ‘real randomness’ in larger processes (or if the ‘randomness’ is aggregated in some central limit theorem-like or law of large numbers-type of way that ‘cancels it out’). I am certain that uncertainty exists in my mind, and that a good amount of it could be reduced with the right information. But I also like the information theory/coding problem where we treat some sources of uncertainty as things we don’t care about the fine details of (the precise order of grains of sand doesn’t matter for an image of a family on a beach). In this case we care about the grains of sand having some plausible structure (not all the black grains clustered together, but uniformly spread out, with some hills). This maps well to the way classical GANs or VAEs operate by injecting noise to fill in these details that capture an incredible amount of entropy as far as the raw signal goes, but is constrated the way recent GANS, Conformers, or MAEs don’t typically use any ‘input noise’ at all to generate all of the fine structure.

This was fun but it’s getting a bit rambley now, and I’m done for the day. I guess that’s what happens when I read and try to connect everything that I’ve done.