(Michael Chinen)

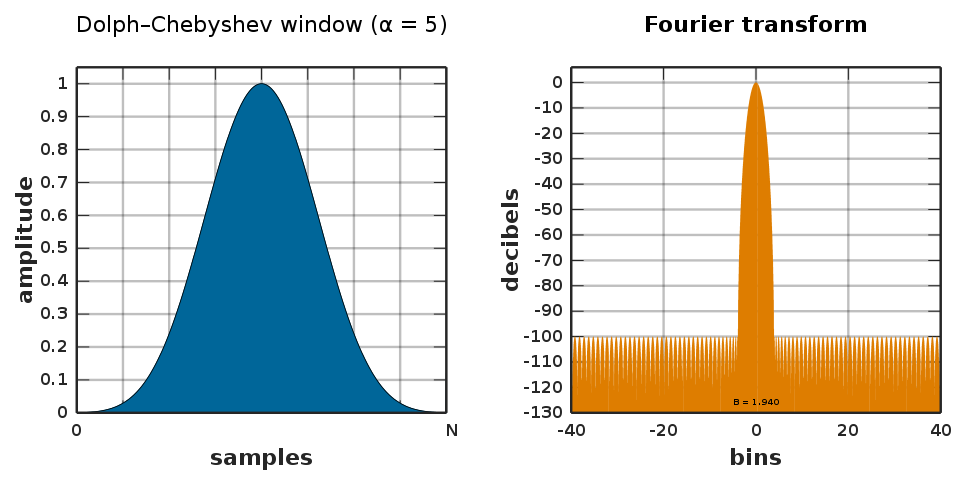
The choice of a window in a discrete Fourier transform (DFT) is an art due to tradeoffs that it implies. When the time domain signal with a single frequency (e.g. a sine-tone) is transformed into the frequency domain, it creates a lot of other ‘phantom’ frequencies called sidelobes. The no-window choice of the rectangular window has a -13 dB sidelobe whenever the frequencies of the signal are not perfectly divisible by the window length (but when they are there are no sidelobes). In practice, for audio processing, I see Hann and Hamming windows being used. The Hamming window is my personal favorite due to a very high sidelobe rejection of over -40 dB, and has a raised edge, which destroys less information. Also Richard Hamming is cool (cf. see: Bell labs – Shannon’s manager and the famous asker of the ‘Hamming Question’) .

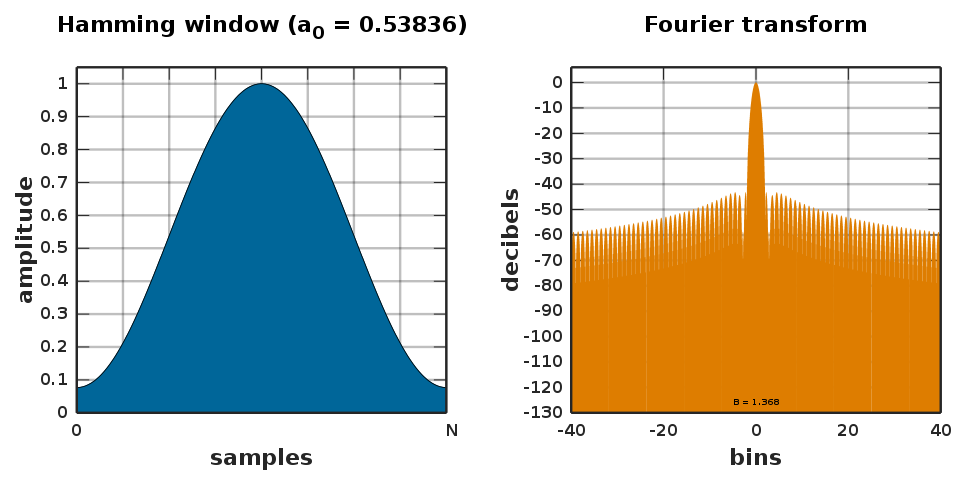
When I think about windows I usually think about the Fourier transform of these windows. But they don’t tell the full story. Phase, as usual, complicates everything. Notice how the sidelobes are themselves periodic. Without even analyzing anything, this implies there is some complex rotation going on, and the DFT is just ‘sampling’ this rotation at regular intervals. This is why you can use a rectangular window on a signal with a certain frequency and get no windowing artifacts or sidelobes – in this case the sampling/aliasing of the window happens to fall exactly where the complex values are the same. So as you move away from the exactly-aligned frequency to other frequency, the sidelobes ‘pop’ into existence.

Generally, DSP practitioners just pick one window for an application and stick to it. In theory, we could use an adaptive window to reduce sidelobe confusion, but it is not simple. Using an convolution directly on the waveform in ML processing is effectively assuming a fixed window, (and often comes with windowed preprocessing) as in TasNet or wav2vec. Something about this feels like a Bayesian problem since the choice of window provides different uncertainties conditional on the application and properties of the signal. It’s fun to think about how an adaptive window might work. Adaptive filters are fairly common, of course (and virtually all ML-processing is adaptive), but somehow the first thing that touches the signal – the window – is more difficult to touch. Perhaps this has to do the the relative stability that a fixed window brings. But if you look at picking the window for each frame to reduce the uncertainty. The ‘easy’ way out, is to use a very high sampling rate and/or Mel spectrogram, which smoothes out the sidelobes considerably for the high frequencies. Anyway this is a brainstorm, and something to look at further in the future.

The other thing I want to dig further into is the complex phasor for these windows. In other words, how the real and imaginary values evolve with respect to frequency for the window. My guess is that it looks a lot more steady than the sidelobes in the typical magnitude frequency domain that we commonly look at, especially if we looked at the Dolph-Chebyschev window which is designed to have flat sidelobes. This is not a big leap in perspective, and probably something people have looked at, but I don’t recall it being discussed in my signal processing education. I’d like a 3blue1brown-style animation of this.