19
Jun 25
13:09
How much should I value browsing the web?
A frugal mindset can develop anti-frugal tendencies, or ‘cheapness’, that optimize for lower cost at the expense of too much time or accepting poor quality or discomfort. True frugality should consider the tradeoff beyond all of these factors. Personally, I still struggle with analysis paralysis in the metaphorical candy aisle. It’s helped to have a minimum dollar amount or rate, under which I should not bother deal hunting under. However, in practice, it depends on the specifics of what you’re buying and there are properties of the stopping problem that are not so cut and dry. For example, walking instead of taking an Uber has health benefits (and running does even more but then you get a sweaty shirt). For web browsing though, it feels like it’s mostly opportunity cost, so it might be easier to look at.
Like a lot of people, I feel that I waste too much time in front of a screen browsing in a loop without good reason other than looking for stimulus. I’ve tried the timer based and jail browser extensions, but they don’t quite do it for me (actually, they make me value bad browsing more because of the scarcity, even if it’s artificial). So this is an exercise to convince myself that it’s really not very valuable, and that the valuable parts are not where I’m spending my time.
The browsing data
I looked at 148,405 web pages on my personal desktop browser since January 1, 2025 to June 19, 2025. Some single-page visits like google maps take up 10-50 history entries with url rewrites each time you scroll, but I’d estimate that’s about 50% of the total, so let’s say 50k pages conservatively are intentional page views, or an average of around 280 per day and probably 100-1000 on any given day. This doesn’t include phone usage, but as a desktop guy, my phone web browsing is almost non-existent. This is also only my personal profile where I don’t do any ‘serious’ work. I don’t really use social media other than reddit, and I guess this one area that is probably very different from others.
Here’s a table of the top 25 domains with my viewing numbers, constructed from a vibe coded and verified script to export and analyze firefox history that made some assumptions about view length if there were not a series of repeated domain hits:
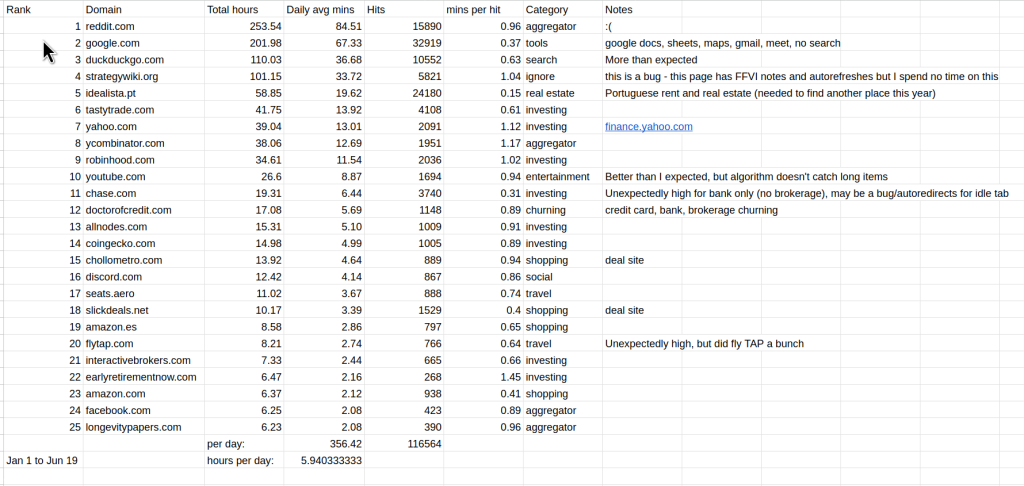
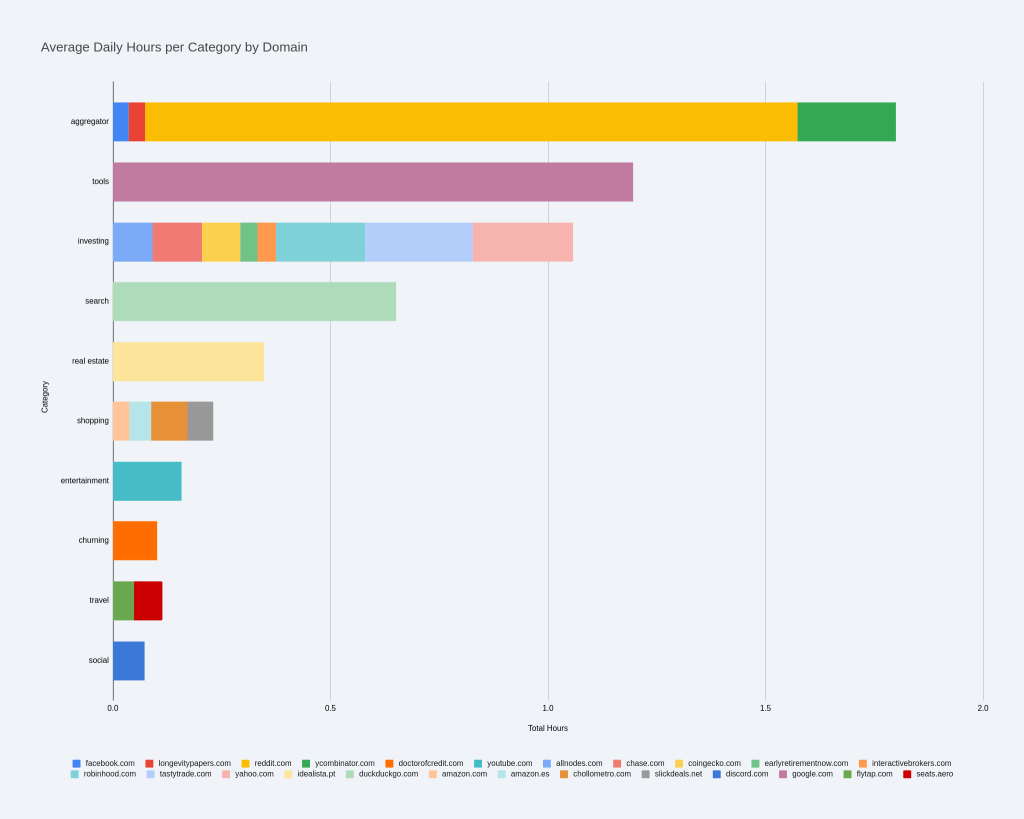
It’s devastating, but insightful. I spend about 6 hours a day on ‘personal browsing’. I think if it’s overestimating it’s by 10 to 25% at most, so let’s say 5 hours. Ten years ago or so when I used the jail timebox extension, it also showed me the usage, and it was not as bad as this (IIRC it was at 3-4 hours). I also have days when I don’t browse much or at all (<10% of days), so this means the peak usage is likely over 9 hours. This doesn’t include my work profile browsing or time in the terminal/apps, but I would estimate my total daily screen usage at an average of about 8 to 12 hours.
Wait, but the diamonds in the rough make it worth it, right?
I didn’t review every page, but I scrolled over the entire history to see what content I would actually rate as valuable today. I found that only about once a week I found a truly interesting web page. It was usually from Hacker News or my own longevitypapers.com or some tech announcement. Of course, this is from the page title only, so I may be missing some valuable pages. Anyway, here are the pages that have enough utility that I would feel comfortable recommending to friends or colleagues. Maybe that’s not the right bar, but I felt like 99% of the remaining pages weren’t useful. There were a lot of things that were too specific to be interesting, or had a consistent but relatively low value, or too personal or embarrassing (like most things related to health, shopping diligence, travel, review spiraling, personal finance/trading, real estate hate browsing, churning, fitness).
- Andrej Karpathy: Software Is Changing (Again) – YouTube
- Biotech financing: divide and reset | Nature Biotechnology
- Longevity Papers 2025-06-13: A single factor for safer cellular rejuvenation – YouTube (self)
- A senior engineer’s guide to the system design interview | Hacker News
- Building Effective AI Agents \ Anthropic
- Best math book you’ve ever read? : math
- Seed investing in biotech
- Vibe coding Menugen
- Options Trading Series: Part 13 – Year 2024 Review
- Full paper analysis: Epigenetic editing at individual age-associated CpGs affects the genome-wide… – YouTube (self)
- Vitalist Bay
- Which single proven proof, if internalized, would teach the most amount of modern mathematics? : math
- The LongBio Report 2025 (self)
- Being “just a copy” is good enough for me : transhumanism
- Introducing Anthropic’s AI for Science Program \ Anthropic
- Veo 3 and Imagen 4, and a new tool for filmmaking called Flow | Hacker News
- More Than Just Quite OK – Data Compression Nerds Hate This One Trick – media.ccc.de
- Turn any old laptop into a personal server | Jan 24 | Medium – used this to recycle my 2011 macbook as a permanent server for longevitypapers.com
- https://longevitypapers.com (self)
- DuoBook: Generate bilingual stories to learn any language | Hacker News
- Nattokinase: Plaque Reversing Supplement, or Biased Science? – YouTube
- Core Pathways of Aging – LessWrong
- Sony Bravia Bouncy Balls – 4K Remastered – YouTube
- I use Cursor daily – here’s how I avoid the garbage parts | Hacker News
I also found that while HN is still pretty useful in producing valuable page views, reddit is almost completely lacking value except for a few cases: finding local information, or niche subreddits. Both HN and reddit have been degrading in quality with the obvious LLM comments and posts, especially ones that are emotion-inducing and personal (e.g. “I’m dying of cancer and just figured out a million dollar side hustle that i want to pass to my kids”). Fortunately these still have identifiable tics (it’s not just em-dashes, it’s a whole new paradigm), but that’s not going to last long once these are labeled as negative examples.
I value these links at about $5000, generously. That is, if you told me that all my memories of these posts would be deleted, I would pay you $5000 to prevent it. Naively, spending 6 hours a day for $29 in return is not great. Yes, this is ignoring all the small values I got from other pages that didn’t make the list, but I don’t think they are worth that much more.
To be fair, I value experiencing the content of the page differently than the information content and knowledge criteria I used to make the list. But I also feel that the attraction there is more of an addiction than something I actually enjoy most of the time, and that I would get more out of having a better balance between browsing and doing other things, either in front of the computer or outside.
Changing the loop
Another expected finding was the other categories of things I can and should cut out or limit to a slice, including financial spinning (stocks/options/crypto), and browsing aggregators like reddit/HN.
Personal investing is a tricky one. Some of these are are very low but positive ROI, which makes it hard to stop. Filtering by the largest absolute return (instead of ROI) for churning items would be useful (>1% APY brokerage bonuses) and limiting trading data to open and close only would be a reasonable start. I’ve been selling far OTM 0DTE SPX options with stops as ERN describes, so in theory it should be hands off, but in practice it’s easy to get sucked back in to see how the day is going, especially when things are volatile. This is a 1-2% APY ROI on top of the returns from a 3-fund portfolio with relatively low risk (surviving the +10% S&P500 day in March relatively unscathed makes me more confident in that), so it’s significant. But it may be that the mental load is just not worth it if I can’t stick to the time limits.
One hack that has been useful for me, and sustainable over several years is digesting this information for these categories in a language I’m learning, which is Japanese, Portuguese, or German. It’s harder to spend excessive time in a second language, and combined with the educational benefit, it makes the value more balanced. I get a value multiplier on the original content by reading Portuguese subreddits, watching a Daily Show-like German show (ZDF Magazin Royale), and watching Japanese news (TBS), and this seems sustainable. I could apply this to other domains as well.
It took quite a while to review and analyze my web history, but it feels like a healthy checkup I should do yearly. I’ve confirmed my worst suspicions that most days the browsing I do is neither fun, interesting, or valuable. One thing I didn’t expect to find was although Hacker News was where the highest quantity of valuable pages came from, only once every few weeks there was something valuable enough to save, and these items were usually in Google News or my LinkedIn feed, which I’ve usually avoided as a part of my social media avoidance. So it might make sense to reduce reddit and HN and sprinkle a small amount of LinkedIn. One of the draws of these tech sites since slashdot was that it’s industry info so keeping up is probably good for you on some level, but it might be worth challenging that again. Maybe it’s also worth going back to regular news outlets, although they are lacking the discussions. Reading books is another thing that may fill this gap. Will keep thinking on this.
As a concrete and testable goal, When I rerun this analysis again (maybe in months, or end of the year), I want to reduce my ‘aggregator’-type browsing to 1 hour a day, unless I am getting some new value out of it. I want to reduce ‘investing’ and ‘real estate’ as well. I thought shopping and churning were going to be higher, and they might just not be captured by the top 25 domains, but I’m going to work on the largest obvious offenders first. Eventually, I might make a fun project out of it to turn deal hunting and credit card/bank/brokerage churning by vibe coding a personally-tuned push-based solution.
In the future, it might be fun to do this with an estimate range of ROI per page. This probably isn’t enough data to do something like this. Maybe there’s a power-law distribution where it’s just the one post you happen to see that is worth a million bucks so you should keep doing this. I doubt it, but I’d like to consider it further since humans tend to be risk averse and not great at using intuition to reason about events of very low probabilities. But for the non-intuitive category, I can definitely say that being frugal with the quality of my time is something I will need to be proactive about and remind myself where I sit with some explicit analysis like I’ve done here today.